2D-transformaatiot

2D-transformaatiot ovat sellaisia metodeja, joilla kuvan sijaintia, kokoa, muotoa ja kuvakulmaa voidaan helposti muuttaa. Tämä kevyt johdatus noudattelee löyhästi Processing.orgin 2D Transformations -tutoriaalia, joka on hieman kattavampi katsaus aiheeseen. Voit myös tutkia Mehackitin workshop-materiaalia.

Siirto (Translation)

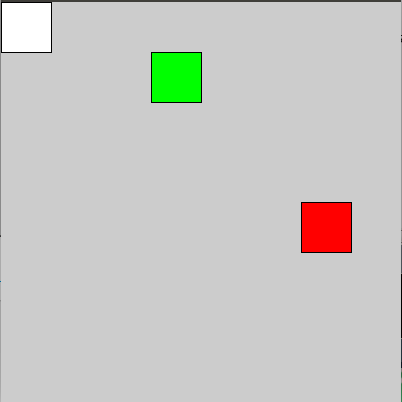
Translate-metodi siirtää kaiken kuvassa näkyvän uuteen nollakohtaan, joka annetaan sille parametrina. Uusi nollakohta lasketaan suhteessa senhetkiseen nollakohtaan (aluksi ruudun vasen yläkulma). Eli alla olevassa esimerkissä ensimmäinen translate(30, 20) muuttaa ruudun (0, 0)-pisteeksi eli origoksi pisteen (30, 20). Siirto on näppärä tapa siirtää kaikkea ruudulla olevaa kerralla saman verran - näin meidän ei tarvitse muuttaa yksittäisten kuvioiden koordinaatteja käsin.

size(400, 400);
rect(0, 0, 50, 50);    // piirretään valkoinen neliö alkuperäiseen origoon

translate(300, 200);
fill(255, 0, 0);
rect(0, 0, 50, 50);    // piirretään punainen neliö uuteen origoon
                       // (0+300, 0+200) = (300, 200) on siis nyt (0, 0)

translate(-150, -150);
fill(0, 255, 0);
rect(0, 0, 50, 50);    // piirretään vihreä neliö uuteen origoon
                       // (300-150, 200-150) = (150, 50) on siis nyt (0, 0)

Kierto (Rotaatio)

Tutustutaan seuraavaksi hieman kiertoon ja siihen, miten erilaisia transformaatioita voi yhdistellä. Havainnollistetaan myös rotaatiota draw-loopin sisällä.

int i = 0;

void setup(){
  size(500, 500);
  noStroke();
}

void draw(){
  fill(255, 10);
  rect(0, 0, width, height);      // kts. häivytys: piirretään läpikuultava neliö 
                                  // koko ruudun päälle
  fill(100, 100);                 // valitaan väriksi läpinäkyvä harmaa

  translate(width/2, height/2);   // siiretään kuva ruudun keskipisteeseen
  rotate(radians(i));             // muunnetaan i radiaaneiksi ja käännetään 
                                  // kuvaa i verran
  rect(0, 0, 50, 50);             // piirretään neliö kohtaan (0, 0)
                                  // joka on siis nyt ruudun keskellä

  i++;                            // kasvatetaan i:n arvoa yhdellä
                                  // kun i menee yli 360, on kuvio 
                                  // kierähtänyt kerran itsensä ympäri
}

Radians-metodi muuttaa parametrina annetut asteet radiaaneiksi.

Nyt neliö pyörii yhden kulmansa ympärillä. Voit kokeilla hieman muuttaa neliön sijaintia. Mitä tapahtuu, jos sijoitat neliön (0, 0)-pisteen sijaan kohtaan (-25, -25)? Entä mitä tapahtuu, jos vaihdat translate- ja rotate-metodien paikkoja?

Mittakaavan muutos (skaalaus)

Muutetaan seuraavaksi kuvan mittakaavaa ja lisätään mukaan hieman interaktiivisuutta käyttämällä hiiren x-koordinaattia.

void setup(){
  size(500, 500);
  background(255);
  noStroke();
}

void draw(){
  fill(255, 100);
  rect(0, 0, width, height);    // häivytys

  fill(100, 100);
// skaalataan kuva suhteessa mouseX:n arvoon
// voit kokeilla muuttaa vakion 0.2 arvoa
  scale(mouseX/(width*0.2));    
  rect(0, 0, 100, 100);
}

Viistoutus (shear)

Kokeillaan seuraavaksi viistouttaa kuvaa. Tämä tapahtuu kahden metodin avulla: shearX ja shearY.

void setup(){
  size(500, 500);
  background(255);
  noStroke();
}

void draw(){
  fill(255, 100);
  rect(0, 0, width, height);    // häivytys

  fill(100, 100);
// viistoutetaan kuvaa sekä x-akselin että y-akselin suhteen
// riippuen kulloisestakin hiiren sijainnista
// voit myös kokeilla muuttaa vakiota 0.9
  shearX(mouseX/(width*0.9));
  shearY(mouseX/(height*0.9));
  rect(50, 50, 100, 100);
}

Transformaatioiden suoritusjärjestys

Huomasit ehkä jo aiemmin, että mikäli rotate-metodi suoritetaan ennen translate-metodia, lopputulos on erilainen kuin jos translate suoritetaan ennen rotate-metodia. Yleisin suoritusjärjestys transformaatioille on Translate, Rotate, Scale, mutta voit toki eksperimentoida!

Processing-ympäristössä on myös olemassa kaksi matriisioperaatiota: pushMatrix ja popMatrix. pushMatrix ikään kuin asettaa nykyisen ruudun päivitettäväksi ja popMatrix palauttaa muokatun ruudun näkyville. Näiden kahden metodin toimintaan voit tutustua tarkemmin Processing.orgin 2D Transformations -tutoriaalissa jos haluat, mutta tässä vaiheessa riittää hyvin tieto siitä, että on hyvä kutsua pushMatrix-metodia ennen transformaatioiden tekemistä ja niiden tekemisen jälkeen kutsua popMatrix-metodia.